Character Encodings
13 Sep 2020 | categories: blog
prev: Ruby: Enumerable & Enumerator | next: Ruby Modules
I sat down a few weeks ago to write a small blog post on what the UTF encodings are, I mainly wanted to talk about why UTF-8 is the most common encoding on the internet and also how it worked but after a couple of minutes I felt it would be good to also explain what ASCII is because it’s interesting in its own right and understanding its story would help people appreciate the problem that Unicode solves.
I then thought that a primer on what came before ASCII would be interesting too because ASCII was created to solve some problems, a few hours of research later and it became apparent that there is a lot of history when it comes to encoding text. Basically what I’m say is I didn’t intend for this post to go as far back in history as it does but apparently I found all of this shit interesting so I am presenting everything I have learnt to you for your reading pleasure.
Now, I did briefly go over character encodings in my post on Control Characters but in this post I’m casting a wider net, you can think of this as more of an extension of that post. Quite a lengthy extension. So buckle up and let’s go back in time.
visual codes
Before we get round to chatting about computers and character encoding using bits I think it would be good to get an overview of what telegraphy is as it would help set the stage for later, let’s go over some visual codes that have been used throughout the ages.
signal fires
Millennia ago, if you wanted to convey a message over long distances without sending a messenger you really didn’t have many options, The Great Wall of China for example made use of signal fires or drum beats. If some trouble were afoot then a look-out could light their fire, and look-outs all along the wall would see this fire and know they need to light theirs too, this relay system helped spread the message a lot faster than someone on a horse could.
The only problem is that a fire can’t really convey much information, it’s either lit or it isn’t. On or off. Either there is trouble coming or everything is fine.
To be fair to signal fires they did the job but if you wanted to ask your mate a few kilometers away “do you fancy grabbing some lunch later?” you couldn’t do it with a signal fire, unless of course you agreed ahead of time that lighting a fire meant an invitation to lunch.
Everyone needs to agree on what lighting this fire means, the message they want to convey is encoded in the flames so to speak. Having said that by 200BC flag signalling had been developed so look-outs had a wider range of messages they could send, so asking your friend to lunch certainly became a lot easier. Speaking of flags…
semaphores
In 1794 a French chap called Claude Chappe invented the Semaphore system, the name is made from the Greek “sema” meaning “sign” and “phore” meaning “carrying”, and the system used flags to send messages. Chappe also used the word “tachygraph” to refer to this semaphore system, tachygraph is made up of “tachy” meaning “swift” and “graphy” meaning “to write”, in other words “fast writer”.

By Lokilech at German Wikipedia - Own work, CC BY-SA 3.0, link
Two flag arms were used in a semaphore, the left was used for messages and the right was used for control characters, this meant that depending on version of the code being used the system could encode 94 or 92 messages in total. This is a lot better then the binary signal fires that were used on the Great Wall of China.
Much like signal fires this system could reliably communicate over long distances with the help of semaphore relay stations, during the height of the French Revolution the first successful message sent using this system was “si vous réussissez, vous serez bientôt couverts de gloire” (If you succeed, you will soon bask in glory) between Brulon and Parce, a distance of 16 kilometers.
The Chappe Code as it was known relied on predetermined messages and phrases that could be strung together, not letters, so there was a code book that each relay station had so the operators knew what message was being sent.
By Courtesy Spinningspark at Wikipedia, CC BY-SA 3.0, link
The French Army preferred to call this semaphore system the “telegraph”, the term was coined by a French statesman called André François Miot de Mélito. “Telegraphy” comes from the Ancient Greek “tele” meaning “at a distance” and “graphy” we know means “to write”. In essence “writing at a distance”.
Telegraphy can be used to describe many forms of communication, signal fires and semaphores can be thought of as optical telegraphy but when telegraphy is mentioned these days most people are referring to electrical telegraphy.
the telegraph
The first experimental electric telegraph system that was used “over a substantial distance” was created by Francis Ronalds in 1816, he laid 8 miles of iron wire in his mum’s garden and sent an electrical signal down it. As cool as this was people were still loving optical telegraphy so the uptake of this new technology was fairly slow despite how groundbreaking it was.
The first commercial electric telegraph patent was submitted in June 1837 by William Fothergill Cooke and Charles Wheatstone. These early telegraph systems were multi-wire affairs, but shit really started getting good when Samuel Morse developed the single-wire telegraph in the United States. Not only did Morse have a hand in improving the telegraph he also invented a way to communicate with it.
Morse code
Back in my post about Control Characters I spoke briefly about Morse Code which is one of the earliest well-known electronically-transmitted character codes. Morse code was invented around 1837 by Samuel Morse as a way to communicate over long distances using the newly-invented telegraph system.

By Hp.Baumeler - Own work, CC BY-SA 4.0, link
Morse Code is a variable-width code which uses a system of four signals to represent text, two of those signals dash and dot were used to represent letters, and the short and long space were used to separate letters and words respectively. There is no need for a code book, you could tap out exactly what you wanted to say. A telegraph key or a “Morse key” was used to tap out these signals which formed messages.
By Rhey T. Snodgrass & Victor F. Camp, 1922 Public Domain, Link
As you can see in the picture above up to four dashes and/or dots were used to represent letters making Morse code a binary system. Dot or dash, only two values.
With one dot or dash you can represent 2 characters as I’ve said, or 2^1 characters. With two dots or dashes you can represent another 4 characters, or 2^2. Add another dash or dot and you get another 8 characters, and if you’re using four dots/dashes then you get another 16.
What I’m getting here is because Morse code is a binary system it follows the powers of two and you could represent 30 characters using up to 4 dots and dashes (2^1 + 2^2 + 2^3 + 2^4).This is grand if you’re dealing with the Roman/Latin alphabet as there are 26 letters.
The interesting thing about this system is the letters that would appear most frequently are given simple codes:
- A = dot dash
- T = dash
- E = dot
Whereas letters that appear infrequently would be more complex:
- Z = dash dash dot dot
- Q = dash dash dot dash
- J = dot dash dash dash
This was intentional, it was to try and cut down on message length as well as help reduce operator fatigue as they would be tapping each letter out.
As technology progressed printing telegraphs were invented, the first of which looked like pianos with characters written on the keys. Instead of tapping out the messages operators could press the corresponding key for a character and the machine would generate the Morse code for that character.

By Ambanmba (talk) - Own work (Original text: I created this work entirely by myself.), Public Domain, link
The intention here was to further cut down operator fatigue, an added benefit was you didn’t need to fully understand Morse code in order to send a message.
Baudot code
Jumping forward a few years to 1870 and Émile Baudot, an officer in the French Telegraph Service, invents the Baudot Code which was initially used with a “piano Baudot keyboard”, which was a small piano-like device that had five keys.
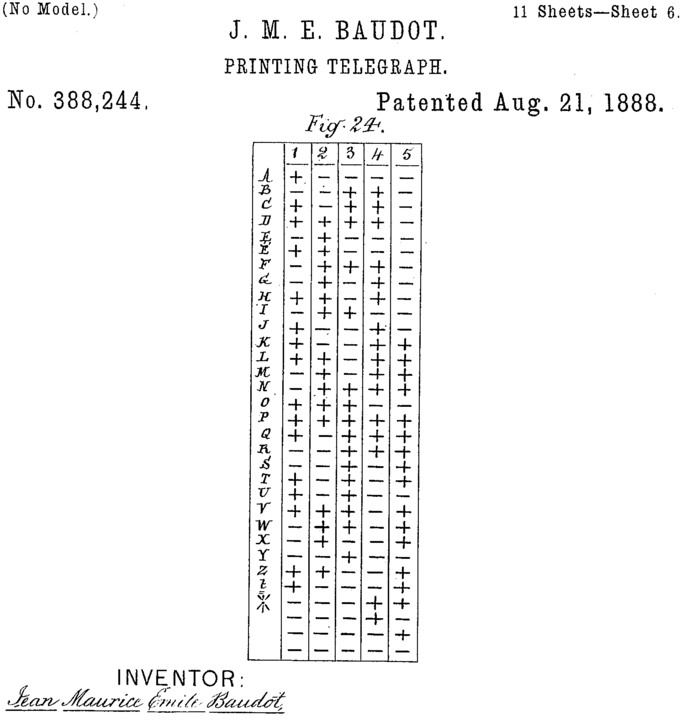
By Jean Maurice Emile Baudot - Image Full patent, Public Domain, Link
This system was a five-bit sequential binary code meaning it encoded characters using 5 bits and unlike Morse code it was a fixed-width code and it needs to always send 5 bits, that means it can represent up to 32 characters (2^5 characters). Seeing as there was some extra code points left over after you take care of 26 letters of the alphabet the system included some punctuation and control characters.
This encoding is what’s known as a Gray Code. A Gray code is one that has it’s consonants and vowels sorted alphabetically and you only need to change one bit to get the next consonant or vowel. The picture above shows the initial Baudot code, but the entire alphabet is sorted to aid with lookup, if we split it out into consonants and vowels you’ll see they differ by a single bit.
vowels
A - 10000
E - 01000
I - 01100
O - 11100
U - 10100
consonants
B - 00110
C - 10110
D - 11110
F - 01110
G - 01010
etc
Operators of a Baudot piano needed to press the keys down that would set the bits for the character they wanted to enter, for example to send the character A they would hold down the key that represents the first bit, which was the third key, and then wait for the machine to click and unlock for the next character. Operators needed to have a steady rhythm to work with the device.
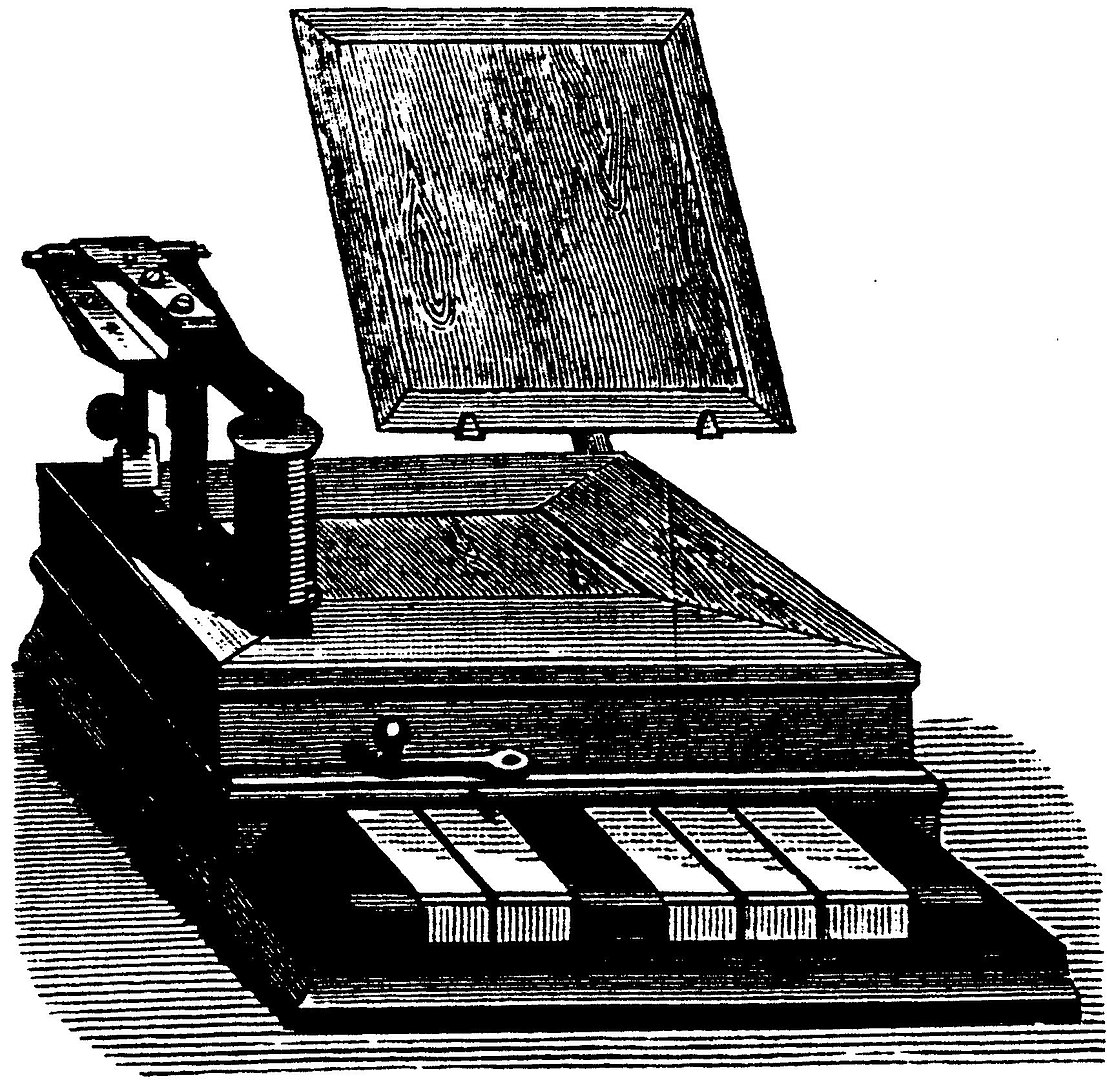
By M. Rothen - Journal telegraphique vol8 N 12 decembre 1884 reprod Eric Fischer History of Character code 1874-1968, Public Domain, link
There are a few variants of the code that can be used for different purposes, like the UK variant and the Continental European variant. The European variant included characters with accents.
Some control characters, also known as shift characters, let operators know what follows aren’t the usual text characters but a different type of character, perhaps punctuation marks or numbers. They would then use another shift character to signal shifting back text characters again.
Murray code
Baudot code was later modified in 1901 by Donald Murray to make it play nicely with Murray’s new invention, a “typewriter-like keyboard”. This keyboard would perforate paper tape, a hole could be thought of as a “one” and a lack of a hole as a “zero”. This meant operators could type out messages in advance then take the resulting tape and feed it to a tape transmitter which would send the message.

By Ricardo Ferreira de Oliveira - Own work, CC BY-SA 3.0, link
Like Morse code, Murray code arrange the code points so frequently used letters would use the least amount of holes. Seeing as the code could be prepared before transmission that meant operator fatigue wasn’t an issue, what he aimed to do with this new arrangement was minimise wear on the machinery.
The only one hole characters:
E - 00001
T - 10000
Some of the two hole characters:
A - 00011
O - 11000
I - 00110
Some of the three hole characters:
B - 11001
C - 01110
G - 11010
And the only four hole characters:
V - 11110
X - 11101
K - 01111
Q - 10111
control characters
As well as rearranging the letters Murray also moved some pre-existing control characters to new positions where they exist to this day, namely the NUL and DEL control characters:
NUL - 00000
DEL - 11111
In ASCII (which we will get to shortly) NUL is indeed 0000000 and DEL is
1111111.
Murray used a row of 5 holes (a DEL character) to represent the start/end of messages, and seeing as a row of holes wouldn’t be very strong the tape could be easily torn to separate the messages.
New control characters were also introduced: carriage return (CR) and line feed (LF). These control characters still exist to this day, but back then they had the job of moving the carriage of a teleprinter back to the first column and moving the sheet of paper up by one line respectively.
western union
Murray’s code was adopted by Western Union and slightly altered to omit some characters and add new control characters such as an explicit space character (SPC) and a bell character (BEL) that rang a bell to let an operator know a message was coming.
teleprinters
By now I hope you’re seeing a pattern of people building on encoding systems which all originally come from the Baudot system, slightly altering them to make it work for their specific purpose or altering it to work with some new technology. That trend continues.
Building on Murray’s “typewriter-like keyboard” a patent was filed in 1904 for a “type wheel printing telegraph machine” by Charles L. Krum which made a practical teleprinter possible and in 1908 the first working teleprinter was produced by the Morkrum Company called the Morkrum Printing Telegraph.

Source unknown
These new teleprinters were basically electronic typewriters that would receive telegraph messages and print out the message on paper to be read by the operator, in turn the operator could type a message on the teleprinter’s QWERTY keyboard to be sent across the wire. No knowledge of the underlying encoding is necessary to communicate with these devices.
ITA2
By 1924 teleprinters were all the rage and a need to standardise became very apparent, the CCITT (now known as the ITU) took the version of Murray code that Western Union had developed and used that as the basis for an international standard known as the International Telegraph Alphabet No. 2, or ITA2 for short.
The United States standardised on a version of ITA2 and called it American Teletypewriter Code or US TTY, and this was used as the basis for 5-bit teletypewriter codes until 7-bit ASCII came about in 1963.
computer age
Early computers were big things without monitors and as such were used with teletypewriters, users would input data using them and the computer would write output onto the same sheet of paper. As previously mentioned US TTY was used as the basis for codes in the early days of computing. You may have noticed in codes that came from Baudot code that there were no lowercase letters, everything was uppercase, this was due to the fact there wasn’t enough code points for lowercase letters.

By ArnoldReinhold - Own work, CC BY-SA 3.0, Link
Teletypesetter
Much like the old “printing telegraphs” which were pianos retrofitted to interface with a new technology, computer users were having to use old telegraphy technology, teleprinters, to interact with computers. An immediate issue was the use of “shift codes” that I spoke about earlier, these were code points that let telegraph operators or machines know the following text needs to be interpreted differently.
If part of a saved message was retrieved from memory then the computer has no way of knowing which character the bits represent unless it searches back through the text to find a shift code (or lack thereof). This led to the creation of a 6-bit encoding known as Teletypesetter (TTS) code, the code was first demonstrated in 1928 and saw widespread use through out the 1950s.
In TTS the additional 6th bit stored the shift state of the character, this code was of use to teleprinters too not just computers. If a single character got corrupted then only that character was affected and not the rest of the message until the next shift code was sent which was the case with older codes. On top of that the 6-bit code could also represent uppercase and lowercase letters, digits, symbols, and typesetting instructions such as “bold” or “italics”.
ASCII
We have now reached the 1960s and teleprinter technology had improved to the point where longer codes were no longer as cost prohibitive as they once were, not only that but computer manufacturers wanted to get rid of ITA2 and its shift codes altogether.
In October of 1960 the American Standards Association
(ASA), now
known as the American National Standards Institute (ANSI), started working on a
replacement for ITA2, a new 7-bit code. This 7-bit code would give us 2^7 (128)
code points to work with from 0x00 to 0x7F in hexadecimal.
Hexadecimal numbers are going to be coming up a lot more as we move through the
post so I’ll differentiate between them and decimal numbers by including a 0x
at the start of the number to save me typing “in hexadecimal”.
The ASA considered using an 8-bit code as it would enable efficiently encoding two digits with binary-coded decimal, however that would mean always storing and transmitting 8 bits when 7 bits would have done the job. For this reason they stuck with a 7-bit code.
The new code was called American Standard Code for Information Interchange, or ASCII for short, and it was released in 1964 and very rapidly became the standard teleprinter code. It’s worth noting that this was the last code developed with telegraph equipment in mind, seeing as computer networks and the internet would play a bigger role in communication in the coming decades.
By Anomie - Own work, Public Domain, Link
95 of the 128 code points were used for printable characters, i.e. lowercase and uppercase letters, numbers, symbols, and punctuation. The rest were unprintable control characters which were for use with teleprinters, the majority of these codes are now obsolete however some are still used to this day, such as:
- NUL - null
- CR - carriage return
- LF - line feed AKA newline
- HT - horizontal tab
- DEL - delete
sorting text
ASCII was not only developed with telegraph equipment in mind but it was also designed to aid with programming. The letters were in numerical order according to their code point which meant sorting text alphabetically just meant sorting numbers.
Char | Hex | Binary
----------------------
A 41 100 0001
B 42 100 0010
C 43 100 0011
etc
For example A is 0x41 in hexadecimal and C is 0x43. The letter A is less
than C.
If you’ve had a look at the chart above you might also have noticed that there is only a one bit difference between the upper- and lowercase versions of a letter, the sixth bit.
Char | Hex | Binary
----------------------
A 41 100 0001
a 61 110 0001
^
B 42 100 0010
b 62 110 0010
^
C 43 100 0011
c 63 110 0011
^
etc
The space character comes before any of the printable characters at position
0x20, along with any characters commonly used for separating
words and numbers. This was also done to aid with sorting.
numbers
I mentioned before that an 8-bit code was considered when designing ASCII, it
would’ve helped with encoding numbers using binary-coded decimal, that being an
encoding which uses 4 bits to represent a number. Seeing as they went with a
7-bit code for ASCII they opted to place the numbers in the code points 0x30
through to 0x39.
If I lay them out in a table you might see why this is handy.
Char | Hex | Binary
----------------------
0 30 011 0000
1 31 011 0001
2 32 011 0010
3 33 011 0011
4 34 011 0100
5 35 011 0101
6 36 011 0110
7 37 011 0111
8 38 011 1000
9 39 011 1001
Lopping off the 3 in the hexadecimal representation or the first three bits of
the binary, you get the number it represents. This makes conversion with
binary-coded decimal really simple.
symbols
ASCII introduced a couple of new symbols such as the infamous curly braces {}
and the vertical pipe |, both of which you can find all over programming
languages these days.
Another interesting thing about ASCII is that many of the non-alphanumeric
symbols were positioned to correspond with their shift positions on a mechanical
typewriters. The first mechanical keyboard to have a shift key was the
Remington No. 2, and it shifted the values of 23456789- to "#$%_&'().
Again I’m going to lay these characters out in a table and you can see that they differ by a single bit, the 5th bit, and they are more or less in the same position as they would’ve been on a mechanical typewriter.
Char | Hex | Binary
----------------------
" 22 010 0010
2 32 011 0010
# 23 010 0011
3 33 011 0011
$ 24 010 0100
4 34 011 0100
% 25 010 0101
5 35 011 0101
& 26 010 0110
6 36 011 0110
' 27 010 0111
7 37 011 0111
( 28 010 1000
8 38 011 1000
) 29 010 1001
9 39 011 1001
Oh, and quite nicely 0 lines up with the null character when you remove the first three bits.
Char | Hex | Binary
----------------------
0 30 011 0000
NUL 00 000 0000
control characters
And as I mentioned in my Control Characters post, you could type control characters using your control key and a letter of the alphabet. The letter you use to represent a control character differs from the control character by a single bit, just like the upper- and lowercase letters do. You just flip the most significant bit.
To insert a tab character you can type ctrl-I
Char | Hex | Binary
----------------------
I 49 100 1001
HT 09 000 1001 (horizontal tab)
To insert a newline you can type ctrl-J
char | hex | binary
----------------------
J 4A 100 1010
LF 09 000 1010 (newline)
I won’t go into much detail with control characters but I would like to point
out that ASCII introduced the ESC control character 0x1B, this control character was
meant as a way to signal the next character should “escape” from what it usually
means and take on a different meaning. ESC was intended as a way for people to
extend the character set.
ASCII variations
You might have noticed up until this point that ASCII is very much an encoding that caters to the United States, and english text in particular. American english isn’t the only kind of english kicking around, not to mention there are a load of other languages that use the latin alphabet. The ASCII committee tried to keep other nations needs in mind and left 10 character codes free for national definition.
Due to this need a set of international standards for 7-bit coded character sets was
developed along side ASCII called
ISO-646, I’m not going to go into
the different variants because that would be insane. US-ASCII was intended to be
one of several national variants. For example the UK version varied only
slightly with small adjustments like replacing $ with £.
The point I would like to get across here is there was no “one size fits all” version of ASCII that would cater to everyone.
8-bit ASCII
As technology progressed microprocessors and personal computers with their 8-bit architecture became very popular in the 1980s, this led to the 8-bit byte becoming a standard unit of computer storage. This meant 7-bit ASCII characters were now being stored as bytes meaning the most significant 8th bit was sitting there twiddling its thumbs. 8 bits meant a possible 256 (2^8) characters.
People started using this extra bit to extend ASCII, these variants are known as
extended ASCII character sets. The pluralisation isn’t a mistake, many
different sets were created which led to much confusion and incompatibility.
Indian Script Code for Information Interchange
(ISCII)
and Vietnamese Standard Code for Information Interchange
(VISCII0) are two such examples, both
kept ASCII characters mostly as is in the lower code points 0x00-0x7F but used
the upper code points 0x80-0xFF to define new characters.
Some smart people even created sets that could represent characters in languages that don’t use the Latin alphabet, i.e. ideographs, languages like Korean, Japanese, and Chinese.
One popular ideograph ASCII set was
Shift-JIS which used the codes 0x81
to 0x9F to represent the first of a 2-byte character code. As clever as this
set is it was not the only 2-byte character set popular in Asia, there were three
others. Multiple encodings wasn’t just a Western problem.
ISO-8859
With so many different variants of 8-bit ASCII floating around there became a need for everyone to agree on some sort of standard again, this fell to the International Organization for Standardization (ISO) and International Electrotechnical Commission (IEC).
ISO/IEC 8859 is a joint number from ISO and IEC, 8859 is a set of standards for ASCII and there were 15 parts. The standard adopts the first 128 characters from ASCII, which would use the first 7 bits, then the 15 different parts of the ISO-8859 standard provide definitions for the other 128 characters which make use of the 8th bit.
For example there was ISO-8859-6 which covered common Arabic language characters, ISO-8859-8 covered the modern Hebrew alphabet, and ISO-8859-5 covered the Cyrillic alphabet.
The most popular of these standards was ISO-8859-1 (Latin-1). This one provided complete coverage for most Western languages.
There was no provisions for Chinese, Japanese, or Korean languages as they require thousands of code points, which is sort of problem if you only have 256 code points to work with.
Although these standards helped alleviate some headaches we are still left with the problem of many different encodings and a huge chunk of the world not being catered for. This problem would be solved in time by Unicode, but before we get there I think it’s time to talk about an encoding whose acronym is far too long and a pain to constantly type out.
BCD & EBCDIC
Between 1963-64, around the time ASCII was being developed and unleashed onto the world, a different encoding system called Extended Binary Coded Decimal Interchange Code (EBCDIC) was being developed at IBM. It went on to become the most beloved encoding in the world.
I’m just kidding.
EBCDIC was an 8-bit system and slightly different from all the encodings we have discussed thus far, mainly because it is descended from a code used with punch cards, the 6-bit binary-coded decimal code (BCD), also known as BCDIC. BCD was used in most of IBM’s computers throughout the 1950s and early 1960s, such as the IBM System/360 series. EBCDIC was meant as an extension of BCD.

By Bundesarchiv, B 145 Bild-F038812-0014 / Schaack, Lothar / CC-BY-SA 3.0, CC BY-SA 3.0 de, Link
EBCDIC is a funny little encoding and worth a gander seeing as we are in the area, first let’s talk about punch cards so I can explain what BCD is and then we will circle back to EBCDIC.
IBM & punchcards
In my blog post on Default Text Width I explained that IBM is a company founded way back in the 1896, originally under the name Tabulating Machine Company by a man called Herman Hollerith. Hollerith had invented a machine a couple of years prior which could read data from a punch card, a nifty little invention that made conducting the US Census a lot simpler.
In these early years of the company they focused primarily on creating machines that could deal with punch cards, they releasing an 80-column 12-row punch card in 1928 known as The IBM Card in an attempt to standardise punch cards. Along with these cards they also created a code which was used to represent alphanumeric data, the code would be punched into the rows 0 to 9 and 11 to 12, there was no row 10. Punches 1 to 9 were called rows whereas 0, 11 and 12 were called zones.

By Arnold Reinhold - I took this picture of an artifact in my possession. The card was created in the late 1960s or early 1970s and has no copyright notice., CC BY-SA 2.5, Link
Rows 1 to 9 can be seen in the photo above starting with 9 on the bottom of the card and decrementing upwards, and three special punch “zones” 0, 11 and 12 are at the top of the card.
This code used a single hole to represent a number 0 through 9, and used multiple holes to represent letters and special characters. For example to encode a letter you would need to punch a hole in either zone 0, 11, or 12 followed by a single hole in row 1-9. And if you wanted to encode a special character you would need up to three punches, one or none from 12, 11, 0, then one from 2-7, and finally one in row 8.
Here is a succinct breakdown.
- numbers - single hole:
[0-9] - letters - two holes:
[0, 11, 12] + [0-9] - special characters - two/three holes:
[0, 11, 12, none] + [2-7] + 8
Card integrity was pretty important so the code was designed so holes weren’t too close together, this had a direct impact on the binary encoding of this data too.
BCD
BCD was created as an efficient means for storing this “zone” and “number” punch card data as a 6-bit binary code. With 6 bits you can encode up to 32 characters (2^5). Numbers 1-9 were encoded in the lower four bits (also known as a nibble), and the three special zones 0, 11 and 12 were the higher two bits. BCD codes were not standardised so they varied from manufacturer to manufacturer, even between products from the same manufacturer. I’m going to be using an IBM variant in this post.
For example to encode some numbers just use the lower bits as normal:
Char | Hex | Binary
----------------------
4 04 00 0100
5 05 00 0101
6 06 00 0110
To encode 0, 11, or 12 you need some combination of the higher bits:
Hex | Binary
---------------
10 01 0000 - zone 0
20 10 0000 - zone 11
30 11 0000 - zone 12
So if the letter A is represented by the holes 12 and 1 punched in a card it would have the following binary representation:
Char | Hex | Binary
----------------------
A 31 11 0001
BCD codes did the job for IBM for a few decades until the 1960s when EBCDIC was created.
EBCDIC
As I mentioned EBCDIC was developed around the same time as ASCII, what’s weird is IBM was a big proponent of the ASCII standardisation committee, but the company didn’t have time to create ASCII peripherals such as punch card machines for use with their System 360 computers, this is what gave rise to EBCDIC. Like ASCII EBCDIC could represent a total of 256 characters (2^8).
Their System 360 computer range ended up becoming very popular and thus so did EBCDIC.

By Nikevich (talk) 18:41, 10 March 2011 (UTC) - The same image, with lesser contrast at the top, Public Domain, Link
Above is an IBM punch card with part of the EBCDIC character set punched into it with the character that the punches represent along the top of the card. Although IBMs punch card peripherals could play nicely with this encoding it was, like ASCII, primarily created with computers in mind, so don’t expect any sort of logic or consistency between the punch card code it represents and the binary form.
In BCD the 0, 11, and 12 zones were encoded like this:
Hex | Binary
---------------
10 01 0000 - zone 0
20 10 0000 - zone 11
30 11 0000 - zone 12
And in EBCDIC they are encoded in the higher nibble like this:
Hex | Binary
---------------
C0 1100 0000 - zone 12
D0 1101 0000 - zone 11
E0 1110 0000 - zone 0
Combining zone punches in different ways could be represented too using the higher nibble, I’ll lay them out in a new table.
Hex | Binary
---------------
80 1000 0000 - zone 12 & 0
90 1001 0000 - zone 12 & 11
A0 1010 0000 - zone 11 & 0
The letter A is punched into a card as zone 12 and row 1, so knowing what we
know about EBCDIC the binary encoding would look like this:
Char | Hex | Binary
----------------------
A C1 1100 0001
Conversely, looking up the hexadecimal for a letter in EBCDIC we can work out
what arrangement of punches we need to represent the letter on a card. The
letter S is 0xE2, so that means it’s 1110 0010 in binary. In other words
zone 0 and the digit 2.
Like ASCII, EBCDIC allowed the representation of lower case letters and to get to the upper- or lowercase variant you just needed to flip a bit, so in punch card speak they have the same digit punches but differing zone punches.
Char | Hex | Binary
----------------------
a 81 1000 0001
A C1 1100 0001
b 82 1000 0001
B C2 1100 0001
etc
However the letters weren’t contiguous, there are gaps in both the upper- and lowercase letters in the code.
Char | Hex | Binary
----------------------
o 96 1001 0110
p 97 1001 0111
q 98 1001 1000
r 99 1001 1001
s A2 1010 0010
t A3 1010 0011
I’ll come back to this inconsistency in just a moment.
Numbers were represented by having the highest nibble (4 bits) set to 0xF and using the
lowest nibble for the actual number:
Char | Hex | Binary
----------------------
1 F1 1111 0001
2 F1 1111 0010
3 F2 1111 0011
4 F2 1111 0100
etc
Control characters were represented from 0x00 to 0x40, although not all the
positions were defined so there are gaps. Here are a few characters that we’ve
encountered in other encoding systems:
Char | Hex | Binary
----------------------
CR 0D 0000 1101 - carriage return
HT 05 0000 0101 - horizontal tab
DEL 07 0000 0111 - delete
BEL 2F 0010 1111 - bell
Not all of the character codes defined in ASCII exist in EBCDIC and vice versa, and the ones that were defined typically had a very different code. This along with other inconsistencies led to some problems.
incompatibility
You may have clocked from the few examples I gave there of the EBCDIC encoding that although similar to ASCII in some respects they are for the most part very different beasts, this made writing software that could work with both encodings quite difficult.
sorting
Lowercase letters in EBCDIC came before uppercase letters, whereas in ASCII it is the other way round, this alone was enough to cause problems.
If the following C code were to run using an ASCII encoding it would print the letters A through Z
for (int c = 'A'; c <= 'Z'; c++) putchar(c);
However in EBCDIC due to the problem of codes for letters not being contiguous
this would print characters 0xC1 through to 0xE9, that’s 41 characters
including undefined characters.
missing symbols
I mentioned that ASCII introduced curly braces which are used extensively in programming languages, for example C, these symbols weren’t present in EBCDIC. This made translating source code encoded with ASCII into EBCDIC pretty fucking tough.
On the flip side there were symbols defined in EBCDIC that ASCII didn’t know
about, like the US cent symbol ¢.
too many encodings
So at this point in time we’ve still got too many encodings floating around, even if you got everyone to use a variant of ASCII from ISO-8859 you still run into problems, and now EBCDIC is on the scene and throwing a spanner into the works just for fun.
There’s bound to be a way to solve this problem, and the good news is people started trying to solve it once and for all. Let’s move onto Unicode.
Unicode
Extended ASCII was incredibly successful for many years and the ISO-8859 standard made it possible to represent many world scripts, but the limitations of these encodings were just too annoying to ignore forever. For example you couldn’t have multiple languages in one document, not to mention Chinese, Japanese, and Korean had their own independently developed encodings.
With the Internet rapidly becoming a thing in the 1990s the world was becoming increasingly connected which means people needed to communicate. The problems I’ve mentioned with ASCII prompted work to start in the late 1980s on an encoding that could represent all of the world languages.
history
In August 1988 a guy called Joe Becker (along with help from a few others) published a draft proposal for an “international/multilingual text character encoding system” which they called Unicode. The idea was this encoding was to be a unified universal encoding, and the initial plans were for it to be 16-bit. The assumption was that only characters and scripts currently in use would need to be encoded so 16-bits would be plenty for that.
Over the next couple of years more people joined the group of people working on Unicode, including people from Sun Microsystems, NeXT, and Microsoft. By the end of 1990 a final review draft was ready.
What made this system different was it encodes the graphemes rather than the glyphs of the characters, in other words it encodes the underlying characters and not the renderings of those characters. Unicode provides a code point for the character and leaves the visual rendering up the software, i.e. size, shape, font.
In 1991 the Unicode Consortium was created to maintain and publish the Unicode standard, and in 1991 they published the first of these standards. The standard made the first 256 code points identical to ISO-8859-1 (Latin-1) which made converting existing western text very easy, in other words if you had an ASCII encoded file which adhered to the ISO-8859-1 standard it would work with Unicode with no problems at all.
By June of 1992 the second volume was published which included an initial set of Han ideographs, 20,902 in total. These characters are known as the CJK Unified Ideographs and the inclusion in Unicode meant Chinese, Japanese, and Korean could now be represented in some form.
Unicode 2.0
In 1996 Unicode was updated so it no was no longer restricted to 16 bits, this increase in available bits meant the amount of available code points increased to well over a million. Now Unicode could represent historical scripts such as Egyptian hieroglyphs as well as obsolete languages and characters
Unicode has evolved since then of course with new characters being added over the years and old historic scripts finding their way into the fray too. You still need a way to encode the characters, that’s where UTF comes in.
UTF
Unicode is a standard, it’s not an encoding, Unicode can be implemented by different character encodings and Unicode defines three: UTF-8, UTF-16, and UTF-32. UTF stands for Unicode Transformation Format. UTF-8 and UTF-16 are variable-width encodings whereas UTF-32 is fixed-width. Let’s have a look at them individually starting with UTF-16 seeing as it was the first on the scene.
UTF-16
At the start of the Unicode section I told you that by 1988 work begun on Unicode which eventually spawned a 16-bit encoding, but around the same time a separate encoding standard was being developed which was called ISO 10646 also known as Universal Coded Character Set (UCS).
Now I won’t go into the history of UCS but I brought it up because in 1990 Unicode and UCS were both on the scene but because UCS was complex and the size requirements for UCS was quite large software companies just plain refused to accept the standard. This led to the unification of UCS with Unicode.
The UCS encoding became known as UCS-2 and it differs from UTF-16 because it is
fixed-width and can only encode characters from the Basic Multilingual
Plane.
UTF-16 on the other hand is variable-width, any code points from U+0000 to
U+FFFF are encoded using 2 bytes and anything from U+10000 to U+10FFFF is
encoded using 4 bytes.
Side note: Unicode code points are denoted with U+, but you can think of them
as hexadecimal values.
No. bytes | Codepoints | Byte 1 | Byte 2 | Byte 3 | Byte 4
-------------------------------------------------------------------
2 00-D7FF xxxxxxxx xxxxxxxx
2 E000-FFFF xxxxxxxx xxxxxxxx
4 10000-10FFFF 110110xx xxxxxxxx 110111xx xxxxxxxx
The code points in the gap between U+D7FF and U+E000 are called high
surrogates and they
basically allow you to address characters outside of the Basic Multilingual
Plane, in other words a value falling in this range lets a decoder know that a
further 2 bytes should be read making it a 4 byte sequence.
The Unicode standard permanently reserved the code points U+D800 to U+DFFF
specifically for encoding surrogates and as such they will never be assigned a
character.
To work out a 4 byte sequence for a code point over U+FFFF you:
- Subtract
0x10000from the code point then… - The highest 10 bits are added to
0xD8to get the first 2 bytes, otherwise known as the high surrogate. - The lowest 10 bits are added to
0xDCto get the last 2 bytes, which is known as the low surrogate.
Let’s have a crack at encoding the character 𝐑 which has the code point
U+1D411, I’ve chosen this one because it is over U+FFFF and is going to
require a 4 byte sequence in UTF-16.
In binary U+1D411 is:
0001 1101 0100 0001 0001
Subtracting 0x10000 get us :
0001 1101 0100 0001 0001
- 0001 0000 0000 0000 0000
------------------------
0000 1101 0100 0001 0001
In hexadecimal that is 0x0D411.
Now let’s pull down the 4 byte reference from the table above and insert the binary
for 0x0D411.
Byte 1 | Byte 2 | Byte 3 | Byte 4
------------------------------------------
110110xx xxxxxxxx 110111xx xxxxxxxx
+ 00 00110101 00 00010001
------------------------------------------
11011000 00110101 11011100 00010001
There we have it, the UTF-16 encoding for 𝐑 is 0xD875D811
byte order mark
UTF-16 produces 16-bit code units which means each unit takes up 2 bytes of storage but the order of these bytes depends on the architecture of the computer, this is what’s known as Endianness.
Endianness comes in two flavours: Big Endian, and Little Endian. Big Endian means the bytes are stored in memory highest order byte first, whereas Little Endian stores bytes with lowest order byte first.
For example the number 0x1234 would be stored 0x12, 0x34 in Big Endian
systems and Little Endian systems would store it 0x34, 0x12.
To help with understanding the byte order of a file UTF-16 allows a Byte Order
Mark, the code point U+FEFF is
used for this and it needs to come right at the start of the file. The code
point is for an invisible zero-width non-breaking space.
If the endianness of the system matches the file then the decoder will match the
invisible character and all is well, however if the endianness of the decoder is
different to that of the file then it will match the code point U+FFEF which
is a code point left undefined for this very purpose. The error when decoding
this code point lets the decoder know to perform byte-swapping for the rest of
the bytes in the file.
If the Byte Order Mark is missing then Big Endian architecture is assumed.
UTF-8
UTF-8 was designed as an alternative to an earlier encoding UTF-1, which was a method of transforming Unicode into a stream of bytes however UTF-1 didn’t provide self-synchronisation which made searching for substrings and error correction a bit of a ball ache.
The idea for the UTF-8 encoding was written down on a napkin in a restaurant by Ken Thompson when he was having a meal with Rob Pike, so if it’s easy enough to jot down on a napkin then it should be simple enough to explain here.
As I mentioned UTF-8 is a variable-width encoding meaning the encoding for a
character can be anywhere from 1 byte to 4 bytes, or 8 bits up to 32 bits.
However not all of those bits are used to encode characters, being a
variable-width encoding some of the bits are used to show just how many bytes
make up the character. As you will see in a moment this allows UTF-8 to encode
up to 21-bit values, or U+000000 to U+10FFFF. U+10FFFF being the highest
code point allowed in Unicode, thus UTF-8 can comfortably represent all
characters.
The ASCII set laid out in ISO-8859-1 (Latin-1) is encoded with a single byte in UTF-8, nice and easy so far. This helps with backwards compatibility.
No. bytes | Byte 1
----------------------
1 0xxxxxxx
If a byte starts with a 0 then the following 7 bits represent the ASCII
character.
Moving on to 2 bytes, you can represent the code points U+0080 to U+07FF.
No. bytes | Byte 1 | Byte 2
-------------------------------
2 110xxxxx 10xxxxxx
The beginning of the first byte indicates how many bytes are to follow, a 110
means this is a 2 byte sequence and the first 2 bits in byte two 10 show
that this is a continuation byte.
With 2 bytes you can represent another 1,920 characters which covers nearly all Latin script based languages as well as Greek, Cyrillic, Coptic, Armenian, Hebrew, Arabic, Syriac, Thaana and N’Ko alphabets. This range also covers the Combining Diacritical Marks.
For 3 bytes we just extend the 2-byte sequence, hopefully you can see the pattern emerging here.
No. bytes | Byte 1 | Byte 2 | Byte 3
-------------------------------------------
3 1110xxxx 10xxxxxx 10xxxxxx
With 3 bytes you can represent the code points U+0800 to U+FFFF, the first
4 bits of the first byte again showing how many bytes are in this sequence and
each subsequent byte starting with 10 shows that it’s a continuation byte.
Using 3 bytes we are able to represent the rest of the characters in the Basic Multilingual Plane , this plane contains pretty much every character in common use. This covers most Chinese, Japanese, and Korean characters.
Fancy guessing how 4 bytes are used to represent a 21-bit code? I’m impatient so I’ll just show you.
No. bytes | Byte 1 | Byte 2 | Byte 3 | Byte 4
------------------------------------------------------
4 11110xxx 10xxxxxx 10xxxxxx 10xxxxxx
With 4 bytes we can represent the code points U+10000 to U+10FFFF, the first 5
bits of the first byte showing how many bytes are in this sequence and the
following 3 bytes start with 10 which is to be expected at this point.
With 4 bytes we can represent less common Chinese, Japanese, and Korean characters as well as mathematical symbols, historic scripts, and emojis.
Merging all those tables and you get this:
No. bytes | Codepoints | Byte 1 | Byte 2 | Byte 3 | Byte 4
-------------------------------------------------------------------
1 00-7F 0xxxxxxx
2 80-7FF 110xxxxx 10xxxxxx
3 800-FFFF 1110xxxx 10xxxxxx 10xxxxxx
4 1000-10FFFF 11110xxx 10xxxxxx 10xxxxxx 10xxxxxx
Quite a logical encoding right? If the first byte starts with 0 then it’s a
one byte character, if the first byte starts with 1 it lets a decoder know the
following number of set bits determine how many bytes are in this sequence,
which also provides a way to detect errors such as too many or not enough bytes.
On top of that you can jump into a text file at any point and search forward a
few bytes and find a character. All good stuff.
Let’s have a go figuring out the encoding for ← which is the code point
U+2190. U+2190 falls within the range U+0800-U+FFFF which means we should be able to
represent this in 3 bytes in UTF-8. Let’s just write out the binary for
U+2190.
0010 0001 1001 0000
We have 2 bytes here and in the table above we have room to fit 16 bits in a 3 byte sequence so let’s try that now.
Byte 1 | Byte 2 | Byte 3
-------------------------------
1110xxxx 10xxxxxx 10xxxxxx
+ 0010 000110 010000
------------------------------
11100010 10000110 10010000
That worked out quite nicely because we had 2 bytes to work with, we are left
with the value 0xE28690.
Now you could, if you wanted, represent ← using 4 bytes by padding the original
binary value with zeros to get to 21 bits before encoding it, this is known as
overlong encoding. However the Unicode standard specifies that only the
minimum number of bytes should be used to hold the significant bits of the code
point.
byte order mark
Given what we know about UTF-16 and its Byte Order Mark it makes sense that UTF-8 should have one right? Sort of.
The Unicode standard actually doesn’t require a Byte Order Mark for UTF-8 in fact it goes as far as not recommending using one at all, ASCII encoded using UTF-8 is backwards compatible but when a Byte Order Mark is added this can cause some problems.
If you were to insert one then because U+FEFF is a 2 byte code point it’s
going to result in a 3 byte encoding in UTF-8, feel free to work it out but I’m
going to use one I made earlier: 0xEFBBBF.
UTF-32
If UTF-8 seems to be the most space efficient of the codes we’ve seen so far, let’s look at the worst.
UTF-32 is a fixed-width encoding and uses 32 bits, or 4 bytes, to encode all code points. This is the most space inefficient of the UTF encodings, there will always be at least 11 leading bits that are zero. The upside here is that code points can be directly indexed, much like you could in ASCII. Finding the n-th character in a string is a constant time operation.
Speaking of size, a UTF-32 encoded file would be almost twice the size as the same file encoded using UTF-16, and up to 4 times as large as a UTF-8 encoding.
This simplicity makes working out an encoding in UTF-32 really easy, let’s try a few.
Char | Code Point | Binary
-------------------------------------------------
A U+41 0000 0000 0000 0000 0000 0000 0100 0001
← U+2190 0000 0000 0000 0000 0010 0001 1001 0000
𝐑 U+1D411 0000 0000 0000 0001 1101 0100 0001 0001
Well that was easy, just append zeros to the original binary value until you have 32 bits.
UCS-4
Earlier I told you about the Universal Coded Character Set and how UTF-16 was
related to it, well the UCS standard (ISO-10646) also defined a 32 bit encoding
called UCS-4. UCS-4 could represent each code point in UCS with a 31 bit value,
up to U+7FFFFFFF, due to UCS and Unicode eventually unifying this means UTF-32 is
identical to UCS-4.
There isn’t much else to UTF-32, and in fact that wraps up all of the UTF encodings!
Unicode adoption
We’ve been on a very long journey in this post but an interesting one, it’s one that I didn’t think would be that interesting until I started researching character encodings. I just wanted to talk about how UTF-8 was a clever little encoding, little did I know that many used throughout the years are interesting in their own way.
The encodings we have used throughout history have been dictated by the technology we had at the time, each time we took another little step forward and the encodings changed slightly to meet the new challenges we faced.
From Morse code to Baudot code to Murray code to ITA2 to ASCII to Unicode and all those encodings in between. Each of them created for a specific purpose or to solve a specific problem, eventually the world became so connected a need to unify all of the encodings was too strong to ignore.
ASCII was the most popular character encoding on the internet until UTF-8 passed it at the end of 2007, Google reported in 2008 that UTF-8 was the most common encoding for HTML files.
By Chris55 - Own work, CC BY-SA 4.0, Link
By 2009 UTF-8 had become the most common encoding overall for the internet, and the World Wide Consortium recommends UTF-8 as the default encoding for HTML and XML, and many standards thereafter start supporting UTF-8 with some standards just flat out requiring it.
As of September 2020 95.4% of all web pages are UTF-8 and 97% of the top 1,000 websites are UTF-8. There are languages that are 100% UTF-8 on the internet, these include Punjabi, Tagalog, Lao, Marathi, Kannada, Kurdish, Pashto, Javanese, Greenlandic (Kalaallisut) and Iranian languages and sign languages.
Safe to say Unicode isn’t going away any time soon.



